Quando si esegue una divisione decimale, ci si può chiedere quanti decimali del quoziente dobbiamo calcolare. Se ci viene chiesto di “trovare i decimali del quoziente fino al centesimo”, non abbiamo dubbi. Altrimenti che cosa occorre fare?
Tutto dipende dall’uso che dobbiamo fare del risultato. Se, ad esempio, dobbiamo fare una divisione decimale per calcolare un prezzo in euro, è sufficiente fermarsi ai centesimi; se dobbiamo calcolare una lunghezza in centimetri, in genere è sufficiente fermarsi a un decimale (un decimo di centimetro è uguale a un millimetro), ecc.
Descriviamo i passaggi di calcolo con un esempio: vogliamo trovare il quoziente della divisione di 43,7 per 8.
Quante volte ci sta l’8 nel 43? 5 volte.
5 x 8 = 40; 43 – 3 = 3
A questo punto mettiamo la virgola nel quoziente (dopo il 5) e abbassiamo il 7.
Quante volte ci sta l’8 nel 37? 4 volte.
4 x 8 = 32; 37 – 32 = 5
Abbassiamo uno 0.
Quante volte ci sta l’8 nel 50? 6 volte.
6 x 8 = 48; 50 – 48 = 2
Abbassiamo un altro 0.
Possiamo continuare così fino a quando il resto risulti 0.
Infine, otteniamo: 43,7 : 8 = 5,4625.
Secondo esempio
Risulta essere sempre possibile trasformare la divisione di un numero decimale per un numero intero nella divisione di un intero per un altro intero. Ad esempio, fare la divisione decimale di 43,7 per 8 è uguale a fare la divisione di 437 per 80. Perché?
La spiegazione sta in questa serie di uguaglianze
![]()
Lo schema qui di seguito mostra lo sviluppo della divisione di 437 per 80.
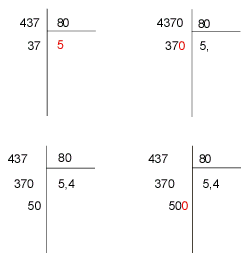
Si procede quindi con le divisioni in colonna. Sull’argomento è possibile vedere anche questa guida sulle divisioni in colonna su questo blog in cui sono presenti altri esempi.